Презентация к уроку по алгебре (9 класс) на тему: Теория вероятностей . Какова вероятность выпадения одного «орла» и одной «решки»? Решение: При бросании одной монеты возможны два исхода – «орёл» или «решка». При бросании двух монет – 4 исхода (2*2=4): «орёл» - «решка» «решка» - «решка» «решка» - «орёл» «орёл» - «орёл» Один «орёл» и одна «решка» выпадут в двух случаях из четырёх.

Cкачать: Урок Сложение и умножение вероятностей. Похожие материалы. Презентация «Свойства функции».

Р(А)=2: 4=0,5. 0,5. Слайд 5. Монета брошена три раза. Какова вероятность выпадения двух «орлов» и одной «решки»? При бросании трёх монет возможны 8 исходов (2*2*2=8): «орёл» - «решка» - «решка» «решка» - «решка» - «решка» «решка» - «орёл» - «решка» «орёл» - «орёл» - «решка» «решка» - «решка» - «орёл» «решка» - «орёл» - «орёл» «орёл» - «решка» - «орёл» «орёл» - «орёл» - «орёл» Два «орла» и одна «решка» выпадут в трёх случаях из восьми.

Р(А)=3: 8=0,3. 75. Слайд 6. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу. При бросании четырёх монет возможны 1.

Благоприятных исходов – 1 (выпадут четыре решки). Р(А)=1: 1. 6=0,0. Слайд 7. ИГРА В КОСТИСлайд 8.

• Презентация для подготовки обучающихся к ЕГЭ и ГИА в 9 классе по теме Решение задач на сложение и умножение вероятностей.
• Задачи на сложение и умножение вероятностей.

Определите вероятность того, что при бросании кубика выпало больше трёх очков. Всего возможных исходов – 6.

11-й класс Разделы: Математика, Конкурс « Презентация к уроку» 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; 24; 25; 26; 27 правила и выбора формулы ( сложение и умножение вероятностей).

Числа большие 3 - 4, 5, 6 . Р(А)= 3: 6=0,5. Ответ: 0,5. Слайд 9. Брошена игральная кость. Найдите вероятность того, что выпадет чётное число очков.

Всего возможных исходов – 6. Вероятность выпадения чётного числа очков равна 3: 6=0,5. Ответ: 0,5. Слайд 1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.

У данного действия — бросания двух игральных костей — всего 3. Благоприятные исходы: 2 6 3 5 4 4 5 3 6 2 Вероятность выпадения восьми очков равна 5: 3. Слайд 1. 1Дважды бросают игральный кубик. В сумме выпало 6 очков.

Найдите вероятность того, что при одном из бросков выпало 5 очков. Всего исходов выпадения 6 очков - 5: 2 4; 4 2; 3 3; 1 5; 5 1.

Благоприятных исходов - 2. Р(А)=2: 5=0,4. 0,4.

Слайд 1. 2ЛОТЕРЕЯСлайд 1. На экзамене 5. 0 билетов, Руслан не выучил 5 из них.

Найдите вероятность того, что ему попадется выученный билет. Руслан выучил 4. 5 билетов. Р(А)=4. 5: 5. 0=0,9. Ответ. 0,9. Слайд 1. СОРЕВНОВАНИЯСлайд 1.

В чемпионате по гимнастике участвуют 2. России, 7 из США, остальные из Китая. Порядок выступления определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. Всего исходов 2. 0. Благоприятных исходов 2.

Р(А)=5: 2. 0=0,2. Ответ. 0,2. 5. Слайд 1. На соревнования по метанию ядра приехали 4 спортсмена из Чехии, 5 из Сербии и 3 из Португалии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что спортсмен, выступающий пятым, будет из Португалии. Решение: Число всех возможных исходов – 1.

Число благоприятных исходов – 3. Р(А)=3: 1. 2=0,2. Слайд 1. 7Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия.

Всего в чемпионате участвует 2. России, в том числе Святослав Кружкин. Найдите вероятность того, что в первом туре Святослав Кружкин будет играть с каким- либо бадминтонистом из России? Toshiba Satellite L350d Manual далее. Всего исходов – 2. Святослав Кружкин с 2.

Благоприятных исходов – (1. Презентация По Информатике На Тему Растровая И Векторная Графика. Р(А)=1. 1: 2. 5 = 0,4. Слайд 1. 8Конкурс исполнителей проводится в 5 дней. Всего заявлено 7.

В первый день 2. 7 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса? Всего исходов – 7. Исполнители из России выступают на третий день. Благоприятных исходов – (7. Р(А)=1. 2 : 7. 5 = 0,1.

Слайд 1. 9ЧИСЛАСлайд 2. Коля выбирает двузначное число. Найдите вероятность того, что оно делится на 5. Двузначные числа: 1. Всего исходов – 9. Числа, делящиеся на 5: 1. Благоприятных исходов – 1.

Р(А)=1. 8: 9. 0=0,2. Слайд 2. 1РАЗНЫЕ ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИСлайд 2. Фабрика выпускает сумки. В среднем на 1. 70 качественных сумок приходится шесть сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. Всего исходов – 1.

Благоприятных исходов – 1. Р(А)=1. 70: 1. 76 . Слайд 2. 3В среднем из каждых 1. Найдите вероятность того, что купленный аккумулятор не заряжен.

Всего исходов – 1. Благоприятных исходов – 1. Р(А)=6: 1. 00=0,0. Ответ: 0,0. 6. Слайд 2. ИСТОЧНИКИ http: // mathgia.

Сложение и умножение вероятностей    Сложение и умножение вероятностей. Дорогие друзья! В этой статье речь пойдёт о решении задач по теории вероятности. Ранее мы с вами уже разбирали некоторые задачи. Для их решения достаточно было знать формулу классической вероятности, то есть понятия благоприятных и всевозможных (равно- возможных) исходов, и применять немного простой «житейской» логики. Основы теории были изложены в статье «Вероятность события. Задачи про такси ..», советую повторить.

Кстати, совсем недавно на блог дополнительно добавлено около 2. Эти задачи вы решите без труда, они в одно действие (на классическую вероятность). Можете их посмотреть: Задачи по теории вероятностей.

Часть 5. Задачи по теории вероятностей. Часть 6. Задачи по теории вероятностей. Часть 7. Задачи по теории вероятностей. Часть 8. Есть задачи немного сложнее (будут на ЕГЭ), для их решения необходимо знать и понимать: правило сложения вероятностей, правило умножения вероятностей, понятие – условная вероятность. В этой статье мы с вами именно такие задачи и рассмотрим.

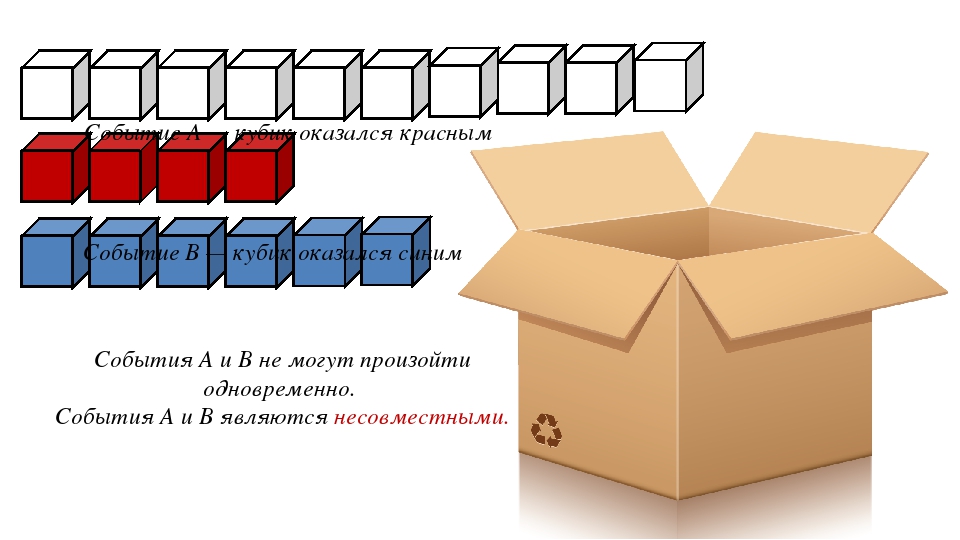
Немного теории (самое необходимое): Определение: События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое. Каждое из этих событий не совместно с другими и совершение одного из них исключает совершение другого (в одном испытании). Определение: События называются совместными, если появление одного из них не исключает появление другого. Пример: из колоды карт будет взята дама и из колоды карт будет взята карта пик. Рассматриваются два события.

Данные события не исключают друг друга — можно вытащить даму пик и, таким образом, произойдут оба события. О сумме вероятностей. Суммой двух событий А и В называется событие А+В, которое состоит в том, что наступит или событие А или событие В или оба одновременно.

Если происходят несовместные события А и В, то вероятность суммы данных событий равна сумме вероятностей событий: Пример с игральной костью: Бросаем игральную кость. Какова вероятность выпадения числа меньшего четырёх?

Числа меньшие четырёх это 1,2,3. Мы знаем, что вероятность выпадения единицы равна 1/6, двойки 1/6, тройки 1/6. Это несовместные события. Можем применить правило сложения. Вероятность выпадения числа меньшего четырёх равна: Действительно, если исходить из понятия классической вероятности: то число всевозможных исходов равно 6 (число всех граней кубика), число благоприятных исходов равно 3 (выпадение единицы, двойки или тройки). Искомая вероятность равна 3 к 6 или 3/6  = 0,5.*Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без учёта их совместного появления: Р(А+В)=Р(А)+Р(В) - Р(АВ)Об умножении вероятностей. Пусть происходят два несовместных события А и В, их вероятности соответственно равны Р(А) и Р(В).

Произведением двух событий  А и В  называют событие А. Вычисляется по формуле: *Умножение  означает, что при некоторых обстоятельствах наступит и событие А, и событие В.

Пример с той же игральной костью: Бросаем игральную кость два раза. Какова вероятность выпадения двух шестёрок? Вероятность выпадения шестёрки первый раз равна 1/6. Во второй раз так же равна  1/6. Вероятность выпадения шестёрки и в первый раз и во второй раз равна произведению вероятностей: Говоря простым языком: когда в одном испытании происходит некоторое событие, и ПРИ ЭТОМ происходит(ят) другое (другие), то вероятности этих событий перемножаются. Задачи с игральной костью мы решали, но пользовались только логическими рассуждениями, формулу произведения не использовали.

В рассматриваемых же ниже задачах без формул не обойтись, вернее с ними будет получить результат проще и быстрее. Стоит сказать ещё об одном нюансе. При рассуждениях в решении задач используется понятие ОДНОВРЕМЕННОСТЬ совершения событий. События происходят ОДНОВРЕМЕННО — это не означает, что они происходят в одну секунду (в один момент времени). Это значит, что они происходят в некоторый промежуток времени (при одном испытании).

Например: Две лампы перегорают в течение года (может быть сказано — одновременно в течение года)Два автомата ломаются в течении месяца (может быть сказано — одновременно в течение месяца)Игральная кость бросается три раза (очки выпадают одновременно это означает при одном испытании)Биатлонист делает пять выстрелов. События (выстрелы) происходят во время одного испытания.

События А и В являются НЕзависимыми, если вероятность любого из них не зависит от появления либо непоявления другого события. Рассмотрим задачи: Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 3. Первая фабрика выпускает 4% бракованных стекол, а вторая –– 2%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. Первая фабрика выпускает 0,3. Вероятность купить бракованное стекло с первой фабрики равна 0,0.

Вторая фабрика выпускает 0,6. Вероятность купить бракованное стекло со второй фабрики равна 0,0. Вероятность того, что стекло куплено на первой фабрике И при этом оно окажется бракованным равна 0,3. Это несовместные события, то есть полученные вероятности складываем: 0,0. Ответ: 0,0. 27. Если гроссмейстер А.

Гроссмейстеры А. Найдите вероятность того, что А. Сказано, что гроссмейстер должен выиграть оба раза, то есть выиграть первый раз И при этом выиграть ещё и второй раз. В случае, когда независимые события должны произойти совместно вероятности этих событий перемножаются, то есть используется правило умножения. Вероятность произведения указанных событий  будет равна  0,6. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,3. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,2. Вопросов, которые одновременно относятся к этим двум темам, нет.

Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. То есть необходимо найти вероятность того, что школьнику достанется вопрос ЛИБО по теме «Вписанная окружность», ЛИБО по теме «Параллелограмм». В данном случае вероятности суммируются, так как это события несовместные и произойти может любое из этих событий:  0,3 + 0,2. Несовместные события – это события, которые не могут произойти одновременно. Ответ: 0,5. 5Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,9.

Найдите вероятность того, что биатлонист первые четыре раза попал в мишени, а последний промахнулся. Результат округлите до сотых. Поскольку биатлонист попадает в мишень с вероятностью 0,9, то он промахивается с вероятностью 1 – 0,9 = 0,1   *Промах и попадание это  события, которые при одном выстреле не могут произойти одновременно, сумма вероятностей этих событий равна 1. Речь идёт о совершении нескольких (независимых) событий. Если происходит событие и при этом происходит другое (последующие) в одно время (испытание), то вероятности этих событий перемножаются. Вероятность произведения независимых событий равна произведению их вероятностей.

Таким образом, вероятность события «попал, попал, попал, попал, промахнулся» равна 0,9. Каждый из них может быть неисправен с вероятностью 0,0. Найдите вероятность того, что хотя бы один автомат исправен. Найдем вероятность того, что неисправны оба автомата. Эти события независимые, значит вероятность будет равна произведению вероятностей этих событий: 0,0. Событие называется невозможным, если оно никогда не произойдет в результате опыта.

Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий. Определение: События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью. В приведенном выше примере появление красного и зеленого шаров – равновозможные события, если в коробке находится одинаковое количество красных и зеленых шаров.